History Of Mathematics – Numeric Systems
Humans created the concept of mathematical numbers to describe quantities such as the size of an animal herd with a limited amount of effort, and to put these quantities in order.
The development of numeric systems was preceded by a lengthy process. This is due to the level of abstraction required in associating the same terms with the same quantities of objects in order to find a generally binding description of quantities; for example not only three cups are associated with the number three, but also three spoons, three apples, and so on.
Therefore, the number “three” is the result of an abstraction process, which took some time to establish in various cultures. Today still, some indigenous people only use small numbers, which they associate with particular, tangible objects.
Fingers and toes
Humans have always used their fingers for counting. This explains the different increments used in various numeric systems. Some cultures used the five fingers of one hand or ten fingers of both hands, while others used the ten toes in addition to the fingers. The numeric system in ancient Egypt, for example, was based on increments of ten, while the Maya and Aztec counted in increments of 20.
The French number quatre-vingt (four times 20) meaning 80, and a similar form used in Danish, are traces of this numeric system that uses increments of 20. The Babylonians were an exception: they used increments of 60. The graduation of hours into 60 minutes of 60 seconds each and angular units are still used.
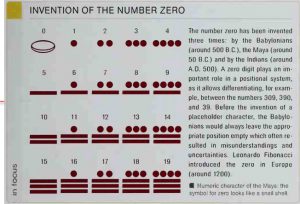
Additive and positional system (place-value notation)
In an additive system, the value of a number is given by the sum of its digits, where the order of number signs does not affect the value. Such a system was used by the Romans among others, but large numbers are difficult to express and the system is completely unsuitable for multiplication, fractional arithmetics, and advanced mathematics. The positional system differs, as the value of individual digits depends on the position.
This is seen in our decimal system (e.g., 1,243 = 1 x 10^3 + 2 x 10^2 + 4 x 10^1 + 3). The latter originates from India and was imported into Europe by Arabic mathematicians. The Babylonian sexagesimal system is based on the same principle (e.g., 243 = 2×602 + 4x 601 + 3).

ISSUES TO SOLVE
THE ISHANGO BONE is a notched bone that is at least 20,000 years old, found in Central Africa in 1950. Some researchers suspect the first traces of an arithmetic system, while others suggest the notches might represent a moon calendar.
